Lecture 3: Maximum Likelihood (Oxford machine learning)

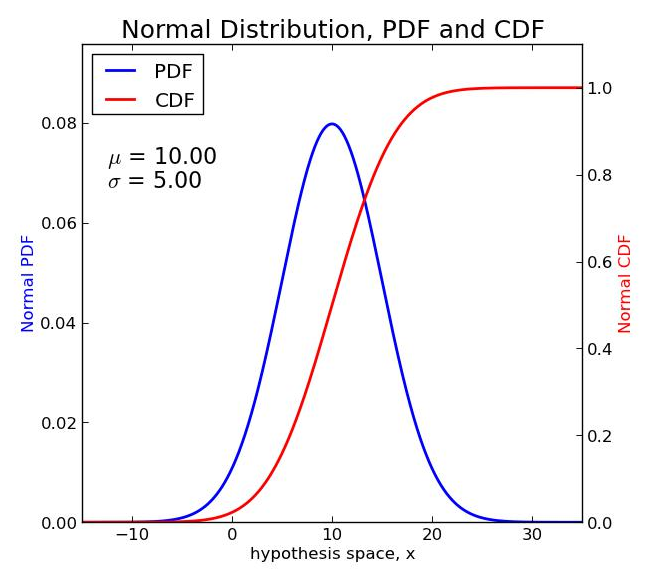
Univariate Gaussian distribution

The pdf of a Gaussian Distribution

$$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2} \qquad x\sim\mathcal{N}(\mu,\sigma^2)$$

where $\mu$ is the mean or center of mass and $\sigma^2$ is the variance.

Covariance, correlation and mutivariate Gaussians

Covariance

The covariance between two rv’s $X$ and $Y$ measures the degree to which $X$ and $Y$ are related. Covariance is defined as

$$cov[X,Y] \overset{\underset{\mathrm{\triangle}}{}}{=} \mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])] = \mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y]$$

Expectiation

$$\mathbb{E}(X)=\int xp(x)dx = \mu \approx \frac{1}{N}\sum_{i=1}^{N}x^{(i)}$$

왜 $\mu$가 저렇게 estimate 될 수 있을까? 먼저 우리는 저 적분을 각각의 $x$에 해당하는 $y$값을 쌓은 결과의 합으로 예측하자. 그러면 $P(x)$를 histogram estimator로 생각해 줄 수 있다. 이를 위해 우리는 먼저 function $\delta$를 정의해준다.

$$p(x)\approx\frac{1}{N}\sum_{i=1}^{N}\delta (x-x^{(i)})$$

where $N$ is the total number of points and each $x^{(i)}$ are the frequency point.

일반적으로 $\delta$는 Dirac Delta Function으로 불린다.

There are three main properties of the Dirac Delta Function.

$$\delta(t-a)=0, \quad t\ne a$$ $$\int_{a-\epsilon}^{a+\epsilon}\delta(t-a)dt = 1, \quad \epsilon>0$$ $$\int_{a-\epsilon}^{a+\epsilon}f(t)\delta(t-a)dt=f(a), \quad \epsilon > 0$$

From the properties of the $\delta$ function, with $f(x)=x$ and $x^{(i)}=a$:

$$\int f(x)\delta(x-a)dx=f(a)\\ \int x\delta(x-x^{(i)})dx=x^{(i)}$$ $$\mathbb{E}(x)=\int xp(x)dx \approx \int x \frac{1}{N}\sum_{i=1}^{n}\delta(x-x^{(i)})dx = \frac{1}{N}\sum_{i=1}^{N}x^{(i)}$$

참조1 참조2

covariance matrix

If $X$ is a $d$-dimensional random vector:

$$\text{cov}[\mathbf{x}] \overset{\underset{\mathrm{\triangle}}{}}{=} \mathbb{E}[(\mathbf{x}-\mathbb{E}[X])(\mathbf{x}-\mathbb{E}[x])^T] = \begin{bmatrix} var[X_1] & cov[X_1,X_2] & \cdots & cov[X_1,X_d] \\ cov[X_2,X_1] & var[X_2] & \cdots & cov[X_2,X_d] \\ \vdots & \vdots & \ddots & \vdots \\ cov[X_d,X_1] & cov[X_d,X_2] & \cdots & var[X_d] \\ \end{bmatrix}$$

If $\Sigma = cov[X]$,

$$\mathcal{N}(x;\mu,\Sigma) := \frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\times \exp[-\frac{1}{2}(\mathbf{x}-\mu)^T\Sigma^{-1}(\mathbf{x}-\mu)]$$

Bivariate Gaussian distribution example

Assume we have two independent univariate Gaussian variables

$x_1 = \mathcal{N}(\mu_1.\sigma^2) \qquad x_2 = \mathcal{N}(\mu_2.\sigma^2)$

We define $\Sigma$ first:

$$\Sigma = \begin{bmatrix} \sigma^2 & 0 \\ 0 & \sigma^2\end{bmatrix} \\ |\Sigma|=(\sigma^2)^2 \\ |a\Sigma| = a^2|\Sigma|$$

Their joint distribution $p(x_1,x_2)$ is:

$$\begin{aligned} p(x_1,x_2)&=p(x_2|x_1)p(x_1) \qquad\qquad \text{because }x_1\text{ and }x_2\text{ are indep.}\\&= p(x_2)p(x_1) \\ &=(2\pi\sigma^2)^{-1/2}e^{-\frac{1}{2\sigma^2}(x_1-\mu_1)^2}(2\pi\sigma^2)^{-1/2}e^{-\frac{1}{2\sigma^2}(x_2-\mu_2)^2} \\&= |2\pi\Sigma|^{-1/2}e^{-\frac{1}{2}\left( \begin{bmatrix} (x_1-\mu_1) & (x_2-\mu_2)\end{bmatrix} \begin{bmatrix} \sigma^2 & 0 \\ 0 & \sigma^2\end{bmatrix}^{-1} \begin{bmatrix} x_1-\mu_1 \\ x_2-\mu_2\end{bmatrix} \right)}\\ &=|2\pi\Sigma|^{-1/2}e^{-\frac{1}{2}\begin{bmatrix} x - \mu\end{bmatrix}^T\Sigma^{-1}\begin{bmatrix} x - \mu\end{bmatrix} }\\ \end{aligned}$$

Likelihood

Let’s assume that we have $n=3$ data points $y_1=1,y_2=0.5,y_3=1.5$, which are independent and Gaussian with unknow mean $\theta$ and variance 1:

$$y_i \sim \mathcal{N}(\theta,1) = \theta+\mathcal{N}(0,1)$$

with likelihood $P(y_1y_2y_3\mid\theta) = P(y_1\mid\theta)P(y_2\mid\theta)P(y_3\mid \theta)​$.

Finding the $\theta$ that maximizes the likelihood is equivalent to moving the Gaussian until the likelihood is maximized.

The likelihood for linear regression

Let us assume that each label $y_i$ is Gaussian distributed with mean $x_i^T\theta$ and variance $\sigma^2$, which in short we write as:

$$y_i = \mathcal{N}(x_i^T\theta,\sigma^2) = x_i^T\theta + \mathcal(0,\sigma^2)$$ $$\begin{align} p(y|X,\theta,\sigma) &= \prod_{i=1}^{n}p(y_i\mid x_i,\theta,\sigma)\\&=\prod_{i=1}^{n}(2\pi\sigma^2)^{-1/2}e^{-\frac{1}{2\sigma^2}(y_i-x_i^T\theta)^2}\\&=(2\pi\sigma^2)^{-n/2}e^{-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i-x_i^T\theta)^2}\\&=(2\pi\sigma^2)^{-n/2}e^{-\frac{1}{2\sigma^2}(y-X\theta)^T(y-X\theta)} \end{align}$$

we can get “probability” of “data” for given “parameters” with constant value $z$ and loss function:

$$\text{prob}(\text{data}|\text{parameters})=\frac{1}{z}e^{-\text{Loss(data,parameters)}}$$

지난번에 사용한 식을 가져와보자.

$$\hat{y}(x_i)=\theta_1+x_i\theta_2\\ J(\theta)=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(y_i-\theta_1-x_i\theta_2)^2$$

우리는 각각의 점에 대해서 하나의 Gaussian 을 놓을 것이다. 각각의 Gaussian의 mean은 $\hat{y}$ 가 될 것이다. 각각의 확률은 각각의 점에서의 Gaussian function 까지의 길이일 것이다. 이렇게 변환시킨다면 문제는 $minimize \ J(\theta)$ OR $maximize \ P(y_1y_2y_3\dots y_n \mid \theta)​$

Maximum likelihood

The maximum likelihood estimate(MLE) of $\theta$ is obtained by taking the derivative of the log-likelihood, $\log \ p(y\mid X,\theta,\sigma)$.

이는 likelihood를 더 컴퓨팅 하기 좋도록 바꿔준다.

The goal is to maximize the likelihood of seeing the training data $y$ by modifying the parameters $(\theta,\sigma)$

$$p(y|X,\theta,\sigma) =(2\pi\sigma^2)^{-n/2}e^{-\frac{1}{2\sigma^2}(y-X\theta)^T(y-X\theta)}\\ log(p(y|X,\theta,\sigma))=-\frac{n}{2}log(2\pi\sigma^2)-\frac{1}{2\sigma^2}(y-X\theta)^T(y-X\theta)$$

The goal is to maximize $log(p(y\mid X,\theta,\sigma))​$ or minimize $-log(p(y\mid X,\theta,\sigma))​$ .

The Maximum likelihood(ML) estimate of $\theta​$ is:

$$\frac{\partial}{\partial\theta}\frac{1}{2\sigma^2}(\mathbf{y}-X\theta)^T(\mathbf{y}-X\theta)=0 \\ \theta_{\text{ML}}=(X^TX)^{-1}\mathbf{y}^TX$$

The Maximum likelihood(ML) estimate of $\sigma$ is:

$$\frac{\partial}{\partial\sigma}[-\frac{n}{2}log(2\pi\sigma^2)-\frac{1}{2\sigma^2}{(y-X\theta)^T(y-X\theta)}] \\= -n\frac{1}{\sigma}+\frac{1}{\sigma^3}{(y-X\theta)^T(y-X\theta)} = 0\\ \sigma^2=\frac{1}{n}{(y-X\theta)^T(y-X\theta)}=\frac{1}{n}\sum_{i=1}^{n}(y_i-x_i^T\theta)^2$$

Making prediction

Given the training data $D=(X,y)$, for a new input $x_*$ and known $\sigma^2$ is given by:

$$P(y\mid x_*,D,\sigma^2)=\mathcal{N}(y \mid x_*^T\theta_ML,\sigma^2)$$

참고

Entropy

Bernoulli

A Bernoulli random variable r.v. $X$ takes values in ${0,1}$

$$\begin{align} P(x \mid \theta)= \begin{cases} \theta && \text{if} \ x=1\\ 1-\theta && \text{if} \ x=0 \end{cases} \end{align}$$

Where $\theta \in (0,1)$. We can write this probability more succinctly as follows:

$$P(x\mid\theta)=\theta^x(1-\theta)^{1-x}=\begin{cases} \theta && \text{if} \ x=1\\ 1-\theta && \text{if} \ x=0 \end{cases}$$

Entropy

In information theory, entropy $H$ is a measure of the uncertainty associated with a random variable. It is defined as:

$$H(X)=\sum_xp(x\mid\theta)logp(x\mid\theta)$$

Example : For a Bernoulli variable X; the entropy is:

$$H(X)=-\sum_{x=0}^{1}\theta^x(1-\theta)^{1-x}log\left[\theta^x(1-\theta)^{1-x}\right]=-\left[(1-\theta)log(1-\theta)+\theta log\theta\right]$$

Entropy of a Gaussian in D dimensions

$$h(\mathcal{N}(\mu,\Sigma))=\frac{1}{2}ln[(2\pi e)^D\mid\Sigma\mid]$$

MLE - properties

For independent and identically distributed (i.i.d.) data from $p(x \mid\theta_0)$( $\theta_0$ is true parameter or parameter of god or parameter generated by nature),the MLE minimizes the Kullback-Leibler divergence:

$$\begin{aligned} \hat{\theta} &= arg\ \underset{\theta}{max}\prod_{i=1}^N p(x_i|\theta) \\&= arg\ \underset{\theta}{max} \sum_{i=1}^N log\ p(x_i|\theta) \\&= arg\ \underset{\theta}{max}\left(\frac{1}{N}\sum_{i=1}^N log\ p(x_i|\theta)-\frac{1}{N}\sum_{i=1}^N log\ p(x_i|\theta_0)\right)\\&=arg\ \underset{\theta}{max}\frac{1}{N}\sum_{i=1}^Nlog\frac{p(x_i|\theta)}{p(x_i|\theta_0)} \\ &\overset{N \rightarrow \infty}{\rightarrow} arg\ \underset{\theta}{min}\int log\frac{p(x_i|\theta)}{p(x|\theta_0)}p(x|\theta_0)dx \\&= arg\ \underset{\theta}{min}\int p(x|\theta_0)log\ p(x|\theta_0)dx - \int p(x|\theta_0)log\ p(x|\theta)dx \end{aligned}$$

---

Course Link

이 글은 Oxford machine learning을 듣고 요약한 글 입니다.