Lecture 6: Logistic regression (Oxford machine learning)

McCulloch-Pitts model

시냅스는 활동전위를 다른 시냅스로 부터 받아서 다른 시냅스로 보내준다. 이와 같은 방식으로 모델을 만든다. 여러개의 파라미터를 받고 이들을 모두 더한 뒤에 function을 통하게 한다. 이 function은 threshold를 정해 이보다 높다면 1 낮다면 0으로 변환시킨다. 일반적인 경우에는 Sigmoid function을 사용한다.

Sigmoid function

sigm($\eta$) refers to the sigmoid function, also known as the logistic or logit function:

$$\text{sigm}(\eta)=\frac{1}{1+e^{-\eta}}=\frac{e^{\eta}}{e^\eta+1} \qquad \eta=X_i\theta$$

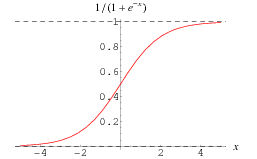
sigmoid 함수의 결과 $\Pi_i$ :

$$\Pi_i=\text{sigm}(\eta)={(y_i=1\vert x_i\theta)}$$

이때의 output $y_i \in \{0,1\}$

Linear separating hyper-plane

결과가 0.5가 될 때가 바로 경계면을 나타낸다.

즉, sigmoid에서는 $\eta$가 0이 되는 지점이다.

이 지점을 discriminant라고 한다.

$$P(y_i=1|X_i\theta)=\text{sigm}(x_i\theta) = \frac{1}{2} \overset{\underset{\mathrm{when}}{}}{\Leftrightarrow} X_i\theta=0$$

Entropy

entropy $H$는 uncertainty를 위한 measure이며 random variable 로 나타내어 진다.

$$H(X)=-\sum_xp(x\vert\theta)\log p(x\vert\theta)$$

Example of Bernoulli

For a Bernoulli variable $X$ , the entropy is:

$$\begin{align} H(x)&=-\sum_{x=0}^1\theta^x(1-\theta)^{1-x}\log[\theta^x(1-\theta)^{1-x}]\\ &=-[(1-\theta)\log(1-\theta)+\theta\log\theta] \end{align}$$

Logistic regression

In logistic regression prediction results are binary. The logistic regression model specifies the probability of a binary output $y_i \in \{0,1\}$ given the input $x_i$ as follows:

$$\begin{align} p(y|X,\theta)&=\prod_{i=1}^{n}\text{Ber}(y_i|\text{sigm}(x_i\theta))\\&=\prod_{i=1}^{n}\left[\frac{1}{1+e^{-X_i\theta }}\right]^{y_i}\left[1-\frac{1}{1+e^{-X_i\theta }}\right]^{1-y_i}\\ \end{align}$$ $$\text{Where}\ x_i\theta=\theta_0+\sum_{j=1}^{d}\theta_jx_{ij}$$ $$\begin{align} \Pi_i&=P(y_i=1|x_i\theta)=\left[\frac{1}{1+e^{-X_i\theta }}\right]\\ 1-\Pi_i&=P(y_i=0|x_i\theta) \end{align}$$

Cross-Entropy

$$\begin{align} C(\theta)&=-\log P(y|x\theta)\\ &=-\sum_{i=1}^{n}y_i\log \Pi_i + (1-y_i)\log(1-\Pi_i) \end{align}$$

Gradient and Hessian

The gradient and Hessian of the negative loglikelihood(NLL), $J(\theta)=-\log p(y\vert X,\theta)$ are given by:

$$\begin{align} g(\theta)&=\frac{d}{d\theta}J(\theta)=\sum_{i=1}^{n}x_i^T(\pi_i-y_i)=X^T(\pi-y)\\ H&=\frac{d}{d\theta}g(\theta)^T=\sum_{i}\pi_i(1-\pi_i)x_ix_i^T=X^T\text{diag}(\pi_i(1-\pi_i))X \end{align}$$

where $\pi_i=\text{sigm}(x_i\theta)$

One can show the $H​$ is positive definite : hence the NLL is convex and has a unique global minimum.

Iteratively reweighted least squares (IRLS)

For binary logistic regression, recall that the gradient and Hessian of the negative log-likelihood are given by

$$\begin{align} g_k=&X^t(\pi_i-y)\\ H_k=&X^TS_kX\\ S_k:=&\text{diag}(\pi_{1k}(1-\pi_{1k}),\dots,\pi_{nk}(1-\pi_{nk}))\\ \pi_{ik}=&\text{sigm}(x_i\theta_k) \end{align}$$

The Newton update at iteration $k+1$ for this models is as follows (using $\eta_k=1$,since the Hessian is exact ):

$$\begin{align} \theta_{k+1}&=\theta_k-H^{-1}g_k\\ &=\theta_k+(X^TS_kX)^{-1}X^T(y-\pi_k) \\ &=(X^TS_kX)^{-1}[(X^TS_kX)\theta_k+X^T(y-\pi_k)] \\ &=(X^TS_kX)^{-1}X^T[S_kX\theta_k+y-\pi_k] \end{align}$$

Softmax formulation

$x_1, \dots,x_d$의 인풋이 파라미터 $\theta_1, \dots ,\theta_d$와 곱해지고 그 것들을 모두 더한 벡터 $x\theta$가 나오고 여기에서 sigmoid fucntion을 통해서 결과를 구하게 된다. 이것이 앞에서 했던 McCulloch-Pitts 모델이다.

이제는 파라미터의 갯수가 증가할 것이다. 단순히 생각한다면 $n$개의 model을 연결해 놓은 것이다. 각각의 model의 아웃풋을 softmax 함수에 넣게 되면 결과가 나오게 될 것이다.

모델이 2개인 경우를 생각해보자. 모델이 2개인 경우 인풋 $x_1, \dots,x_d$ 에 대해서

$\theta_{11}, \dots ,\theta_{1d},\theta_{21},\dots,\theta_{2d}$ 2배가 된 파라미터와 각각 곱해져 각각의 모델의 아웃풋으로 나오게 된다 결과적으로 $\Pi_{i1} , \Pi_{i2}$가 될 것이고 두 값을 더하면 1이 될 것이다.

이때 각각의 값은

$$\Pi_{i1}=\frac{e^{x_i\theta_1}}{e^{x_i\theta_1}+e^{x_i\theta_2}}\\ \Pi_{i2}=\frac{e^{x_i\theta_2}}{e^{x_i\theta_1}+e^{x_i\theta_2}}$$

이는 class 1과 class 2중에서 어떠한 것이 더 결과 값에 적합한지를 판단하는 방식이 될 수 있다.

Likelihood function

INDICATOR:

$$\mathbb{I}_c(y_i)= \begin{cases} 1 \qquad \text{if} \ y_i=c\\ 0 \qquad \text{otherwise} \end{cases}$$

Then:

$$P(y\vert x,\theta)=\prod_{i=1}^{n}P(y_i\vert x_i,\theta)=\prod_{i=1}^{n}\Pi_{i1}^{\mathbb{I}_0(y_i)}\Pi_{i2}^{\mathbb{I}_1(y_i)}$$

when

$$P(y_i=1 \vert x_i,\theta)=\Pi_{i1}^0\Pi_{i2}^1=\Pi_{i2} \\ P(y_i=0 \vert x_i,\theta)=\Pi_{i1}^1\Pi_{i2}^0=\Pi_{i1}$$

Negative log-likelihood

$$C(\theta)=-\log P(y \vert x,\theta)=-\sum_{i=1}^{n}\mathbb{I}_0(y_i)\log \Pi_{i1}+\mathbb{I}_1(y_i)\log\Pi_{i2}$$

Neural network representation of loss

위의 과정을 여러개의 레이어로 생각해 볼 수도 있다.